Title: Pseudoreflection groups in Operator theory and Harmonic analysis
Acronym : PROTHA
Host Institution: Faculty of Mathematics and Computer Science, Jagiellonian University in Krakow, Poland.
Duration: 01/07/2023 - 30/06/2025
Project Summary: In this project, our main focus lies on two problems related to operator theory and harmonic analysis. Although stated separately, both problems are associated to proper holomorphic maps factored by automorphisms. Let D and D be two domains in C^n. We say that a proper holomorphic map f : D --> D is factored by automorphisms if there exists a finite subgroup G⊆Aut(D) such that
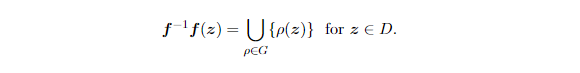
A description of a family F of reducing subspaces is provided for a class of proper holomorphic (which are factored by automorphisms) multipliers on the reproducing kernel Hilbert spaces consisting of holomorphic functions . The family is indexed by the set of equivalence classes of all irreducible representations of the deck automorphism group of the proper holomorphic mapping. Our first goal is to check irreducibility and unitary equivalence for elements of F.
Secondly, let us denote the Bergman projections of D and D by B_D and B_D, respectively. We want to know how L^p regularity of B_D is dependent on the same of B_D, if there is any.
We are also interested in understanding the geometric properties (homogeneity, Lu Qi-Keng property etc.) of D in the light of D. An approach to study operator theory (such as Toeplitz operators etc.) on the function spaces of D (such as weighted Bergman space etc.) using known results for the same of D is on our list as well.
More detailed description of this project can be found here.
This research is part of the project No. 2022/45/P/ST1/01028 co-funded by the National Science Centre and the European Union Framework Programme for Research and Innovation Horizon 2020 under the Marie Skłodowska-Curie grant agreement no. 945339.


